|
|
|
 |
 |
| |
| Volume 21 • Number 2 • 1998 |
| |
•
The Check Positions of Hamming Codes and the Construction
of a 2EC-AUED Code
How Guan Aun and Ang Miin Huey
Abstract.
Hamming Code is the oldest and the most commonly used
single error correcting and double errors detecting code.
For implication, it is constructed over the field GF(2).
For each 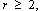 there
is a there
is a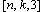 .
Hamming Code where .
Hamming Code where 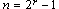 and and
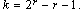 A message word of length k is encoded using a generating
matrix G into a codeword of length n. This amounts to
inserting r parity check digits into the message word.
The positions of the parity check digits in the codeword
are called the check positions of the code (with respect
to G). A received word is then decoded using a parity check
matrix H. If the check positions of the code are in the
A message word of length k is encoded using a generating
matrix G into a codeword of length n. This amounts to
inserting r parity check digits into the message word.
The positions of the parity check digits in the codeword
are called the check positions of the code (with respect
to G). A received word is then decoded using a parity check
matrix H. If the check positions of the code are in the
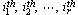 coordinates of the codeword, then the
coordinates of the codeword, then the 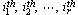 rows of H are called the check rows of the code. We proved
in this paper that for any parity check matrix of a Hamming
Code, there exists a generating matrix G of the code,
such that the check rows of the code are linearly independent. We
believe that this fact is contained implicitly in a paper
of Hamming [7] but we cannot find any explicit proof in
existing literature. Using the above fact, we construct
a 2 EC-AUED code.
rows of H are called the check rows of the code. We proved
in this paper that for any parity check matrix of a Hamming
Code, there exists a generating matrix G of the code,
such that the check rows of the code are linearly independent. We
believe that this fact is contained implicitly in a paper
of Hamming [7] but we cannot find any explicit proof in
existing literature. Using the above fact, we construct
a 2 EC-AUED code.
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|