|
|
|
 |
 |
| |
| Volume 23 • Number 1 • 2000 |
| |
•
On
(4,2)-digraphs Containing a Cycle of Length 2
Hazrul
Iswadi and Edy Tri Baskoro
Abstract.
A diregular digraph is a digraph with
the in-degree and out-degree of all vertices is constant.
The Moore bound for a diregular digraph of degree d and
diameter k is 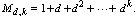 It
is well known that diregular digraphs of order It
is well known that diregular digraphs of order 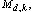 degree degree
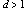 and
diameter and
diameter 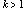 do not exist. A (d,k)-digraph is a diregular digraph of
degree d>1 diameter k>1 and number of vertices one less than the
Moore bound. For degrees
do not exist. A (d,k)-digraph is a diregular digraph of
degree d>1 diameter k>1 and number of vertices one less than the
Moore bound. For degrees 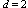 and 3, it has been shown that for diameter
and 3, it has been shown that for diameter 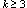 there are no such (d,k)-digraphs. However for diameter
2, it is known that (d,2)-digraphs do exist for any degree
d. The line digraph of
there are no such (d,k)-digraphs. However for diameter
2, it is known that (d,2)-digraphs do exist for any degree
d. The line digraph of 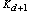 is one example of such (d,2)-digraphs. Furthermore, the
recent study showed that there are three non-isomorphic
(2,2)-digraphs and exactly one non-isomorphic (3,2)-digraph.
In this paper, we shall study (4,2)-digraphs. We show
that if (4,2)-digraph G contains a cycle of length 2 then
G must be the line digraph of a complete digraph K5.
is one example of such (d,2)-digraphs. Furthermore, the
recent study showed that there are three non-isomorphic
(2,2)-digraphs and exactly one non-isomorphic (3,2)-digraph.
In this paper, we shall study (4,2)-digraphs. We show
that if (4,2)-digraph G contains a cycle of length 2 then
G must be the line digraph of a complete digraph K5.
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|