Volume 24 • Number 2 • 2001   • New Proofs of the Uniqueness of Extremal Noneven Digraphs Chjan C. Lim and Gregory K. Van Patten Abstract. The authors give a new graph-theoretic proof of the uniqueness of a class of extremal noneven digraphs, a result originally obtained by Gibson. The method of proof is based on mathematical induction on the number N of vertices in the digraphs, and the fact that there are a limited number of ways to add a new vertex and a fixed number of arcs to a given maximal noneven digraph to obtain a larger maximal noneven digraph. A by-product of this approach is a new short proof of the extremal result: noneven digraphs on N vertices can have at most 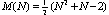arcs. The same approach is then adapted to prove the uniqueness of a class of near extremal maximal noneven digraphs on 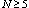vertices. To start the induction process, the authors show directly, without using a computer search, that there is exactly one class of near extremal maximal noneven digraphs on 5 vertices. Full text: PDF