Volume 32 • Number 1 • 2009   • Bayesian Approach for Joint Longitudinal and Time-to-Event Data with Survival Fraction Mohd Rizam Abu Bakar, Khalid A. Salah, Noor Akma Ibrahim and Kassim Haron Abstract. Many medical investigations generate both repeatedly-measured (longitudinal) biomarker and survival data. One of complex issue arises when investigating the association between longitudinal and time-to-event data when there are cured patients in the population, which leads to a plateau in the survival function 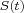after sufficient follow-up. Thus, usual Cox proportional hazard model [11] is not applicable since the proportional hazard assumption is violated. An alternative is to consider survival models incorporating a cure fraction. In this paper, we present a new class of joint model for univariate longitudinal and survival data in presence of cure fraction. For the longitudinal model, a stochastic Integrated Ornstein-Uhlenbeck process will present, and for the survival model a semiparametric survival function will be considered which accommodate both zero and non-zero cure fractions of the dynamic disease progression. Moreover, we consider a Bayesian approach which is motivated by the complexity of the model. Posterior and prior specification needs to accommodate parameter constraints due to the non-negativity of the survival function. A simulation study is presented to evaluate the performance of the proposed joint model. 2000 Mathematics Subject Classification: 62F15, 62G99, 62M05, 62N01. Full text: PDF