|
|
|

|
 |
| |
| Volume 32 • Number 3 • 2009 |
| |
•
Characterization of a Signed Graph Whose Signed Line Graph is S-Consistent
B. Devadas Acharya, Mukti Acharya and Deepa Sinha
Abstract.
A signed graph is a graph in which every edge is designated to be either positive or negative; it is balanced if every cycle contains an even number of negative edges. A marked signed graph is a signed graph each vertex of which is designated to be positive or negative and it is consistent if every cycle in the signed graph possesses an even number of negative vertices. Signed line graph 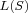 of a given signed graph of a given signed graph 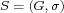 , as given by Behzad and Chartrand [7], is the signed graph with the standard line graph , as given by Behzad and Chartrand [7], is the signed graph with the standard line graph 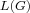 of of  as its underlying graph and whose edges are assigned the signs according to the rule: for any as its underlying graph and whose edges are assigned the signs according to the rule: for any 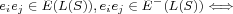 the edges the edges  and and 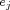 of of  are both negative in are both negative in  . Further, . Further, 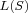 is is  -consistent if to each vertex -consistent if to each vertex  of of 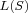 , which is an edge of , which is an edge of  , one assigns the sign , one assigns the sign  then the resulting marked signed graph then the resulting marked signed graph 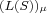 is consistent. In this paper, we give a characterization of signed graphs is consistent. In this paper, we give a characterization of signed graphs  whose signed line graphs whose signed line graphs 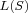 are are  -consistent. -consistent.
2000 Mathematics Subject Classification: 05C22, 05C75.
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|