|
|
|
 |
 |
| |
| Volume 23 • Number 1 • 2000 |
| |
•
Exploiting
Symmetry in Electromagnetic Imaging Problems by using
Group Representation Theory
Deepak
Kumar Ghodgaonkar and Razidah Ismail
Abstract.
Electromagnetic Imaging problems involve development
of an algorithm for estimation of complex permittivities
of a N-cell body from the knowledge of scattered electric
fields at N receiver locations, incident electric fields
at N-cell centroid locations, cell sizes, cell locations
and receiver locations. In this algorithm, it is necessary
to invert a scattering matrix, which relates polarization
current inside the body to scattered electric fields outside
the body. To allow for a large number of cells, it is
necessary to reduce matrix formation and inversion time.
This is achieved by block diagonalization of the scattering
matrix using standard point symmetry 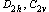 groups
and groups
and 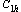 .
For three planes of symmetry, two planes of symmetry and
one plane of symmetry, it is necessary to use groups .
For three planes of symmetry, two planes of symmetry and
one plane of symmetry, it is necessary to use groups 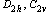 and and
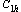 ,
respectively. Group multiplication and character tables
for these groups will be discussed. Due to n ,
respectively. Group multiplication and character tables
for these groups will be discussed. Due to n 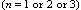 planes of symmetry which depend on
the configuration of the imaging problem regarding cell
locations, cell sizes, receiver locations and transmitter
location, it is possible to block diagonalize the scattering
matrix. In this paper, block diagonalized matrix is derived
for one plane of symmetry which can be generalized to
two or three planes of symmetry. Because of block diagonalization,
it is observed that it is necessary to consider
planes of symmetry which depend on
the configuration of the imaging problem regarding cell
locations, cell sizes, receiver locations and transmitter
location, it is possible to block diagonalize the scattering
matrix. In this paper, block diagonalized matrix is derived
for one plane of symmetry which can be generalized to
two or three planes of symmetry. Because of block diagonalization,
it is observed that it is necessary to consider 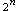 matrices of
matrices of 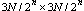 instead of one
instead of one 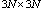 scattering matrix. Hence, it is observed that the matrix
formation time and storage requirements of the scattering
matrix are reduced by a factor
scattering matrix. Hence, it is observed that the matrix
formation time and storage requirements of the scattering
matrix are reduced by a factor 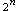 and inversion time is reduced by a
factor of
and inversion time is reduced by a
factor of 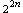 . .
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|