|
|
|
 |
 |
| |
| Volume 25 • Number 1 • 2002 |
| |
•
A
Unicity Theorem for Meromorphic Functions
Huiling Qiu and Mingliang
Fang
Abstract.
In this paper, we study the uniqueness of meromorphic
functions and prove the following result: Let 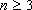 be a positive
be a positive |
integer,
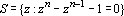 ,
and let ,
and let 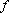 and
and 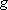 be two nonconstant meromorphic functions whose poles are
of multiplicities at
be two nonconstant meromorphic functions whose poles are
of multiplicities at |
least
2. If 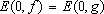 , ,
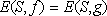 ,
and ,
and 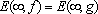 ,
then ,
then 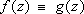 .
This result also answer a question .
This result also answer a question |
of
Gross [4] and
improve some results
of Fang and Xu [1], Yi [14] and Yi [15].
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|