|
|
|

|
 |
| |
| Volume 32 • Number 1 • 2009 |
| |
•
On Finite Groups with Some Conditions on Subsets
Bijan Taeri
Abstract.
Let  be a positive
integer. We denote by be a positive
integer. We denote by 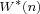 the class of groups the class of groups 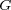 such that, for every subset such that, for every subset 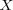 of of 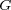
of cardinality  ,
there exist a positive integer ,
there exist a positive integer 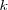 , and a subset , and a subset  , with , with 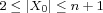 and a function and a function  ,
with ,
with 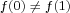 and non-zero integers and non-zero integers 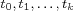 such that such that  , ,
where 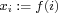 , ,
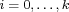 , and , and 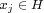 whenever whenever 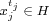 , for some subgroup , for some subgroup 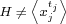 of of 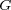 . If the integer . If the integer 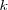
is fixed for every subset
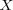 we obtain the class we obtain the class
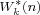 . If one always has . If one always has 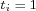 , , 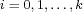 , and , and 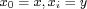 , , 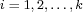 , one obtains the class , one obtains the class 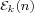 . In
this paper, we prove that . In
this paper, we prove that
(1) A finite semi-simple group has the property 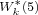 , for
some , for
some 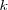 , if and only if , if and only if
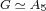 or
or 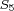 , ,
(2) A finite non-nilpotent group has the property 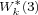 , for
some , for
some 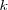 , if and only if , if and only if
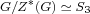 , ,
where 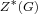 is the hypercenter of is the hypercenter of 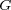 , ,
(3) A finite semi-simple group has the property 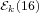 , for
some , for
some 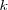 , if and only if , if and only if
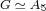 , ,
where 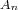 and and 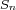 denote the alternating and symmetric groups of degree n
respectively. denote the alternating and symmetric groups of degree n
respectively.
2000 Mathematics Subject Classification: 20F99, 20F45.
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|