|
|
|

|
 |
| |
| Volume 32 • Number 3 • 2009 |
| |
•
Approximation of Gaussian by Scaling Functions and Biorthogonal Scaling Polynomials
S. L. Lee
Abstract.
The derivatives of the Gaussian function, 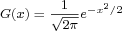 , produce the Hermite polynomials by the relation, , produce the Hermite polynomials by the relation, 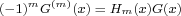 , where , where 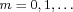 , are Hermite polynomials of degree , are Hermite polynomials of degree  . The orthonormal property of the Hermite polynomials, . The orthonormal property of the Hermite polynomials, 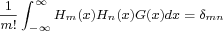 , can be considered as a biorthogonal relation between the derivatives of the Gaussian, , can be considered as a biorthogonal relation between the derivatives of the Gaussian, 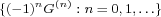 , and the Hermite polynomials, , and the Hermite polynomials, 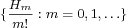 . These relationships between the Gaussian and the Hermite polynomials are useful in linear scale-space analysis and applications to human and machine vision and image processing. The main objective of this paper is to extend these properties to a family of scaling functions that approximate the Gaussian function and to construct a family of Appell sequences of "scaling biorthogonal polynomials" that approximate the Hermite polynomials. . These relationships between the Gaussian and the Hermite polynomials are useful in linear scale-space analysis and applications to human and machine vision and image processing. The main objective of this paper is to extend these properties to a family of scaling functions that approximate the Gaussian function and to construct a family of Appell sequences of "scaling biorthogonal polynomials" that approximate the Hermite polynomials.
2000 Mathematics Subject Classification: 41A15, 41A30, 42C05, 42C15.
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|