|
|
|

|
 |
| |
| Volume 33 • Number 2 • 2010 |
| |
•
Minimal Sequences and the Kadison-Singer Problem
Wayne Lawton
Abstract.
The Kadison-Singer problem asks: does every pure state on the C*-algebra 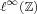 admit a unique extension to the C*-algebra admit a unique extension to the C*-algebra 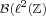 ? A yes answer is equivalent to several open conjectures including Feichtinger's: every bounded frame is a finite union of Riesz sequences. We prove that for measurable ? A yes answer is equivalent to several open conjectures including Feichtinger's: every bounded frame is a finite union of Riesz sequences. We prove that for measurable 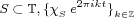 is a finite union of Riesz sequences in is a finite union of Riesz sequences in 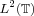 if and only if there exists a nonempty if and only if there exists a nonempty 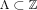 such that such that 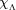 is a minimal sequence and is a minimal sequence and 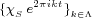 is a Riesz sequence. We also suggest some directions for future research. is a Riesz sequence. We also suggest some directions for future research.
2000 Mathematics Subject Classification: Primary: 37B10, 42A55, 46L05.
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|