|
|
|

|
 |
| |
| Volume 33 • Number 2 • 2010 |
| |
•
Quadratic Diophantine Equation x2 - ( t2 - t ) y2 - ( 4t-2 ) x + ( 4t2 - 4t ) y = 0
Arzu Özkoç and Ahmet Tekcan
Abstract.
Let t ≥ 2 be an integer. In this work, we consider the number of integer solutions of Diophantine equation D :
x2 - (t2 - t)y2 - (4t - 2)t + (4t2 - 4t)y = 0 over  . We also derive some recurrence relations on the integer solutions (xn, yn) of D. In the last section, we consider the same problem over finite fields . We also derive some recurrence relations on the integer solutions (xn, yn) of D. In the last section, we consider the same problem over finite fields 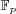 for primes p ≥ 5. for primes p ≥ 5.
2000 Mathematics Subject Classification: 11D09, 11D79.
Full text: PDF
|
| |
|
|
 |
|
|
|
|
|