Volume 33 • Number 3 • 2010   • Normality Criterion Concerning Sharing Functions II Jiying Xia and Yan Xu Abstract. Let F be a family of meromorphic functions in a domain D, and k be a positive integer, and let φ(z)(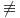 0,∞) be a meromorphic function in D such that ƒ and φ(z) have no common zeros for all ƒ ∈ F and φ(z) has no simple zeros in D, and all poles of φ(z) have multiplicity at most k. If, for each ƒ ∈ F, all zeros of ƒ have multiplicity at least k + 1, ƒ(k)(z) = 0 ⇒ ƒ(z) = 0, ƒ(k)(z) = φ(z) ⇒ ƒ(z) = φ(z), then F is normal in D. This result improves and extends related results due to Schwick, Fang, Fang-Zalcman and Xu, et al. 2010 Mathematics Subject Classification: 30D35. Full text: PDF